「Scan for patterns」

Movivation

• Find a word in a signal of find a item in picture
• The need for shift invariance
  • The location of a pattern is not important
• So we can scan with a same MLP for the pattern
  • Just one giant network
  • Restriction: All subnets are identical

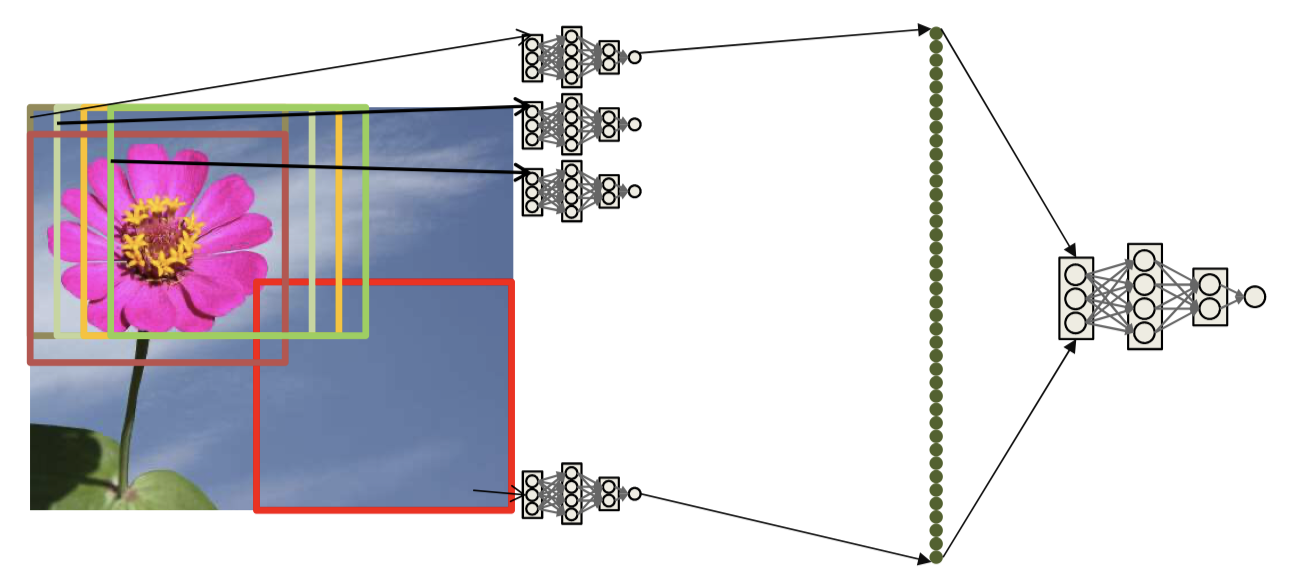
• Regular networks vs. scanning networks
  • In a regular MLP every neuron in a layer is connected by a unique weight to every unit in the previous layer
  • In a scanning MLP each neuron is connected to a subset of neurons in the previous layer
    • The weights matrix is sparse
    • The weights matrix is block structured with identical blocks
    • The network is a shared-parameter model

Modifications

• Order changed
  • Intuitivly, scan at one position and get output, then scan next place
  • But we can also first scan all the position at one layer, then the next layer
  • The result is the same

• Distrubuting the scan
  • Evaluate small pattern in the first layer
  • The higher layer implicitly learns the arrangement of sub patterns that represents the larger pattern
  • Why distribute?
    • More generalizable
      • Distribution forces localized patterns in lower layers
    • Number of parameters
      • Fewer parameters
      • Significant gains from shared computation

Terminology

• The pattern in the input image that each filter sees is its 「Receptive Field」
• Stride
  • Effectively increasing the granularity of the scan
  • This will result in a reduction of the size of the resulting maps
  • Non-overlapped strides
    • Partition the output of the layer into blocks, no overlap
    • Within each block only retain the highest value
• Pooling
  • We would like to account for some jitter in the first-level patterns
  • Max pooling
  • Is just a neuron
• This entire structure is called a Convolutional Neural Network
• The 1-D scan version of the convolutional neural network is the time-delay neural network
  • Used primarily for speech recognition
  • Max pooling optional: jitter matters in speech